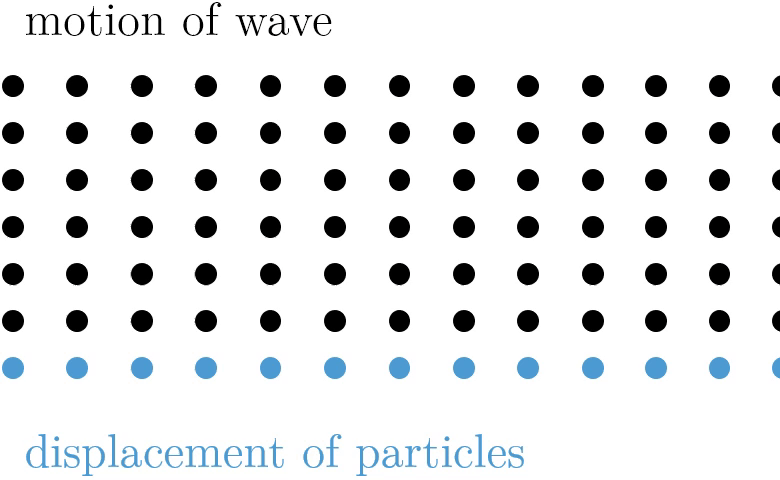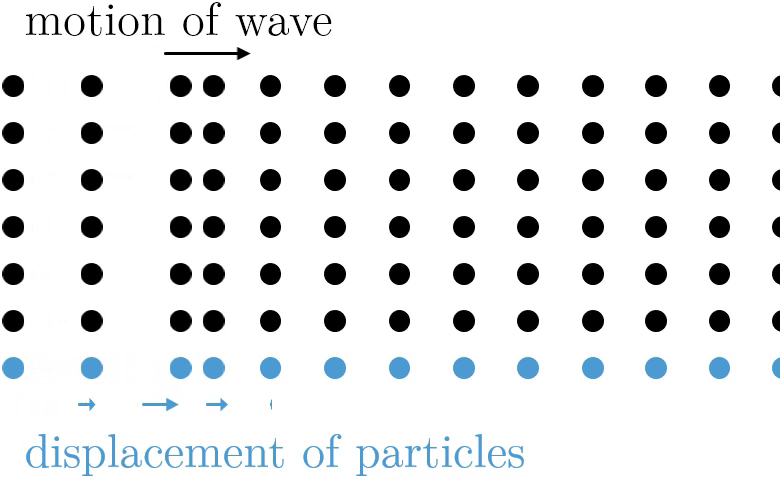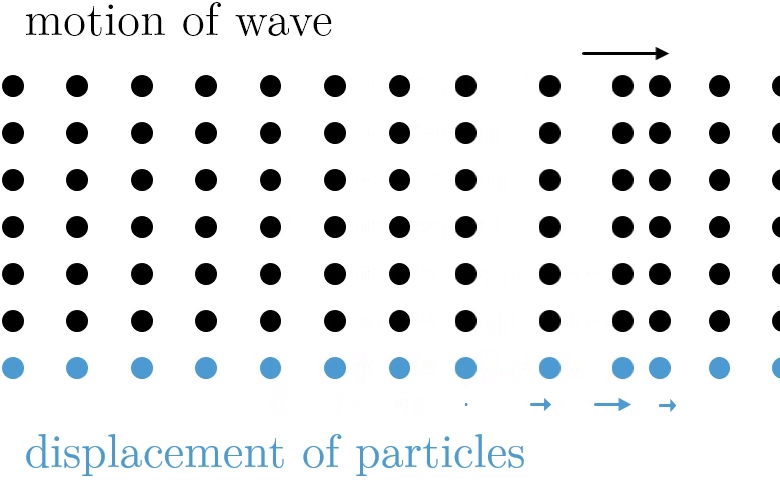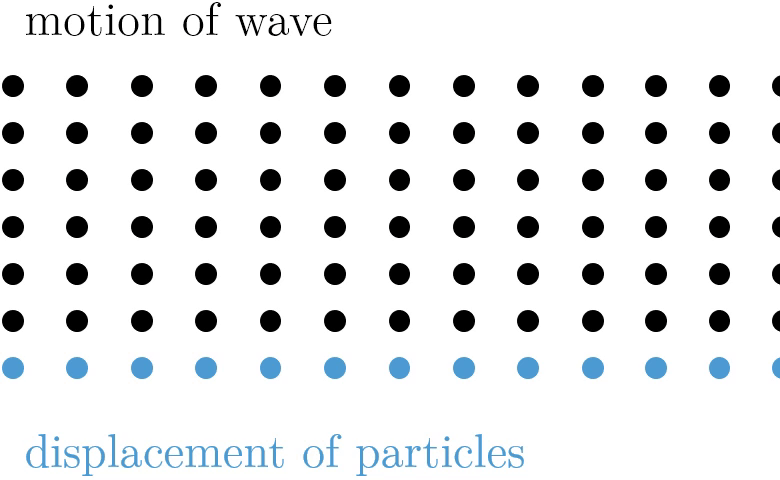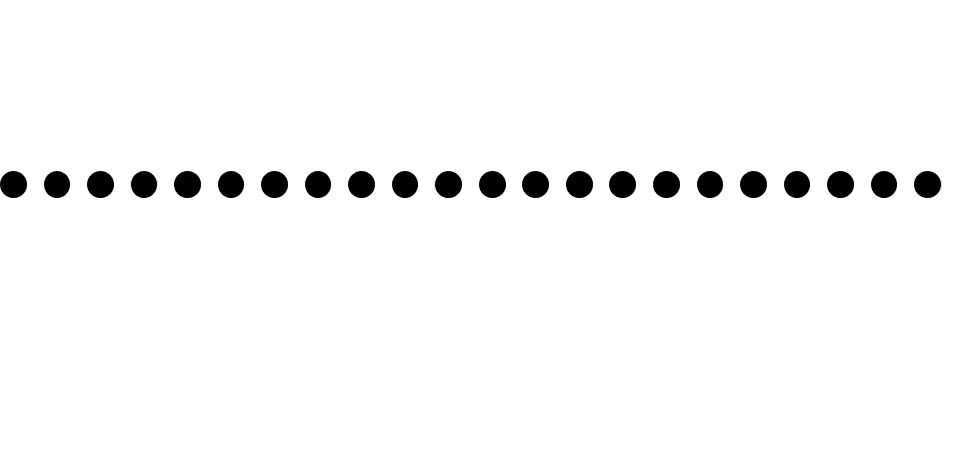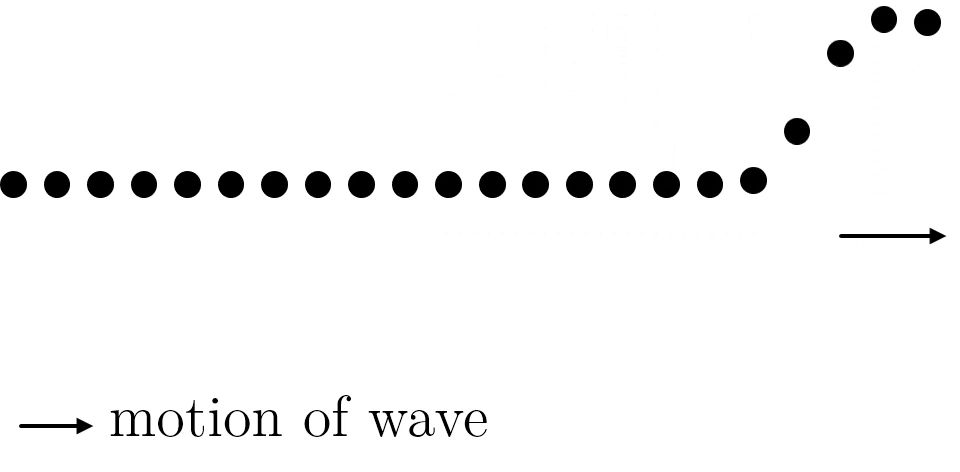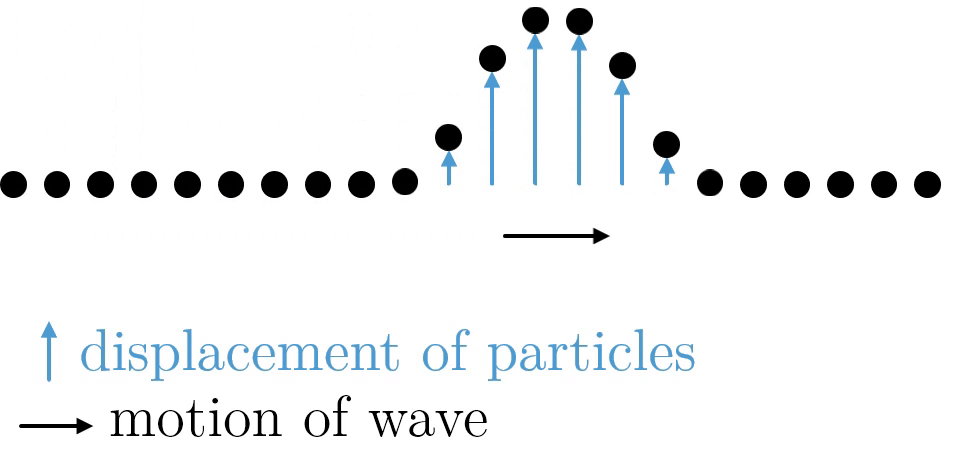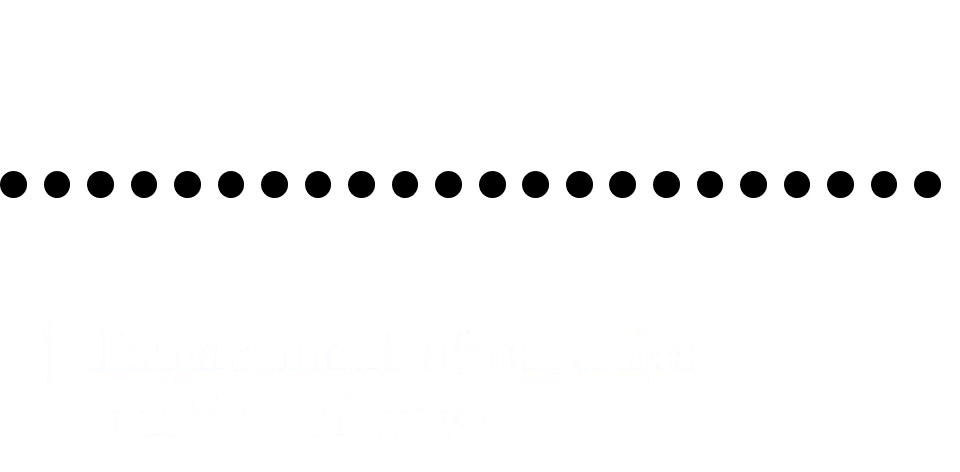Sounds of Music
| Sounds of Music | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | Physics | |||||||||
| Category | Lab | |||||||||
| Description | Teams must construct and tune one device prior to the tournament based on a one-octave 12-tone equal tempered scale and complete a written test on the physics of sound and music concepts. | |||||||||
| Event Information | ||||||||||
| Participants | 2 | |||||||||
| Latest Appearance | 2023 | |||||||||
| Forum Threads | ||||||||||
| ||||||||||
| Question Marathon Threads | ||||||||||
| ||||||||||
| Official Resources | ||||||||||
| Website | www | |||||||||
| Division B Results | ||||||||||
| ||||||||||
| Division C Results | ||||||||||
| ||||||||||
Sounds of Music is an event in which two participants build one homemade instrument, play a scale on their instrument, and explain the physics of sound through a written test. Sounds of Music was previously a Division C event from 1987 to 1993, and Division B event from 1989 to 1993.
The Competition
While much of the work for the Sounds of Music event takes place before the competition, in the form of building, tuning, and practicing, only one part actually counts for Science Olympiad, and that is the competition. The competition is divided into two halves, taking a test and demonstrating your build. The written test is worth 45 points while the instrument is worth 60 points.
This section is not a replacement for the Science Olympiad rules manual. Please read the Science Olympiad rules manual to get exact and official descriptions of each section.
The Written Test
The most points are given for the written test. In a separate room from the instrument testing area, you will have at least 20 minutes to complete at least three questions from each topic:
- Principles of acoustics
- Science terminology involving sound and its production
- Fundamental elements of musical sound; perception of it; resonance
- Design and function of instruments
- Notes, intervals, scales, solfège, time signature, tempo, and related terms about music (i.e. music theory)
The Setup
When you arrive in the competition room, you will have two minutes to set up. This normally isn't a problem, as most instruments are mounted or otherwise ready to play. Some teams do bring xylophones that are not mounted or otherwise connected, and these teams will likely use the majority of the time. The room will likely have very few resources. Some competitions may provide a table or desks to place xylophones on, but it may be smart to bring your own portable table just in case. When setting up, competitors and their instrument have to be 1 meter away from the testing equipment, and failing to do so may result in a penalty.
During the setup time, introduce yourself to your judges. Provide information such as your name, your school name, the type of the instrument you created, and the scale you will be playing.
The Pitch Test
The main instrument testing component will be a pitch score test. You must play a major scale and hold each note for three seconds. The scale must start between F2 and F3 inclusive, and you will have to tell your event supervisor the note name and number of your first note. If you wish to skip any notes, you must declare that beforehand. You will be scored for each note. Multiple attacks on each note are allowed, and the average pitch on each note counts for the score. Notes from the fifth to eighth note of the scale must rise by an octave, so if you began on C3, your scale would be C3, D3, E3, F3, G4, A4, B4, C5, with the fifth note (G4) and beyond more than an octave above the first four notes.
Different levels of competition have different threshholds for how far your instrument can deviate from the target pitch.
| Level of competition | How much error will result in... | |
|---|---|---|
| full credit? | no credit? | |
| Regionals | Less than 10 cents | More than 100 cents |
| States | Less than 7 cents | More than 50 cents |
| Nationals | Less than 3 cents | More than 25 cents |
Two apps were recommended by SOINC for measuring pitch in this event: Google Science Journal and Accord Chromatic Tuner (only available on Android). Pennsylvania has developed its own Internet-based application for measuring pitch.
Song Score Test
You or your partner will play four measures of an arrangement of a piece designated in the Science Olympiad Rule Book on their instrument. The arrangement is provided in the rules manual and is to be played in [math]\displaystyle{ \mathbf{^4_4} }[/math] time. You have 15 seconds to play the arrangement, and event supervisors will assign points based on whether you play the piece within the time limit, and on whether you play with acceptable pitch and rhythm according to the arrangement in the rules manual.
Bonus Pitch
You may choose to play an additional pitch on your instrument for bonus, which is worth 5 points of all-or-nothing credit. The bonus pitch must match the pitch of a note on the staff located an octave or more above or below the range of the scale played in the pitch test.
The Log
The last portion of the event is the log score. You must submit logs containing a list of materials used, data showing how you changed an aspect of your instrument to tune one of your pitches (with at least 5 data points), proper labeling, and a diagram that shows how the instrument is played.
Rubric Overview
The highest score possible for this event, according to the rules, is 105 total. 36 points are awarded in the pitch test, with a maximum of 4.5 points per note; 10 points are awarded for logs; 9 points are awarded in the song score; and 45 points are awarded for the written test. 5 additional points may be earned from bonus.
Written test topics
Sounds of music tests jump from topic to topic depending on the test writers. While the physics of sound is guaranteed to surface, tests have in the past borrowed anything related to sound from a broad umbrella of disciplines beyond merely physics. Both partners should expect to study a variety of content beyond physics, music theory, and instrument building. With this in mind, it is important to not lose motivation because of random questions, as most teams will also face comparable difficulties in grasping seemingly random content.
Physics
What is sound?
From the music of a concert or the boom of a loudspeaker to the creak of a door or the gusts of the wind, sound permeates our world. This is true quite literally—sound occurs when molecules of air vibrate, jostling and pushing against each other. By vibrating, these molecules hit neighboring molecules, which in turn hit and bump their neighbors into vibration as well. This chain of collisions continues to radiate outward from the original source, until the vibrations find their ways to our ears, and our brains perceive these vibrations as sound.
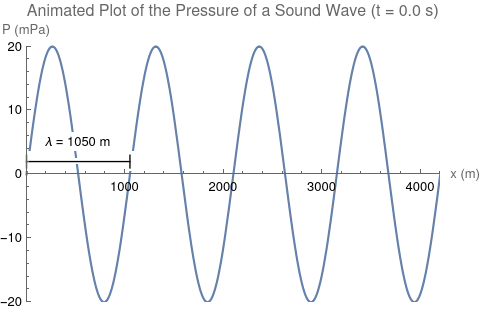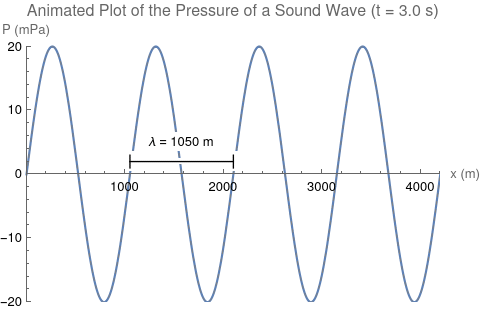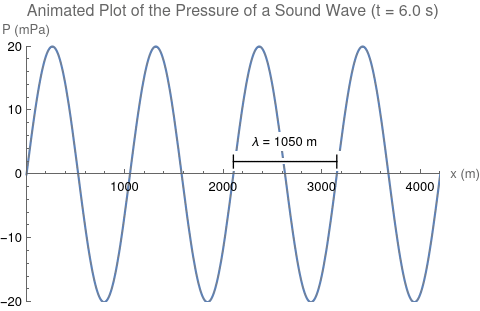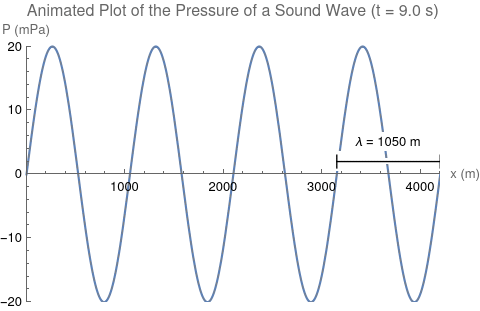
This process of vibration travels through the air in the form of a wave. This wave has certain properties that scientists can measure, such as wavelength, frequency, and speed. The wavelength ([math]\displaystyle{ \lambda }[/math]) of a wave is the length of one cycle of the wave. Wavelength is measured in units of length, such as meters. The frequency ([math]\displaystyle{ f }[/math]) is the number of times the wave repeats per second. For instance, if 1500 cycles of a wave pass by your ear in 3 seconds, your ear will hear a frequency of [math]\displaystyle{ \frac{1500}{3} = 500 }[/math] cycles per second. Another way of saying this is that the wave has a frequency of 500 hertz. Hertz is the SI unit of frequency, abbreviated Hz. The speed ([math]\displaystyle{ v }[/math]) is how fast the wave travels, the distance it travels divided by the time it takes. For example if a wave travels 10 meters in 2 seconds, the wave has a speed of [math]\displaystyle{ \frac{10}{2}=5 }[/math] meters per second. These three quantities are related by the equation [math]\displaystyle{ \lambda f=v }[/math], a fundamental equation in wave physics.
Now that we know sound travels through the air in waves, the next question is "What type of wave is sound?" It turns out that sound is a type of wave known as a longitudinal wave (also called a compression wave), which means that the air particles travel parallel to the direction of the sound wave. Sound waves have areas where the air particles are closer together (called compressions) and areas where the air particles are farther apart (called rarefactions). This is caused by differences in air pressure, which cause the air particles to bunch up or move away from each other. At compressions, the air pressure is higher than normal atmospheric pressure while at rarefactions, the air pressure is lower than normal atmospheric pressure. When you talk, you change the air pressure in the air around your mouth, and these changes in air pressure travel as a wave to another person's ears.
Longitudinal waves are not the only type of wave vibration. There are also transverse waves, where the motion of the wave is perpendicular to the motion of the medium. The movement of a violin string, for example, is a transverse wave. Some media are even capable of carrying both types of waves, like a Slinky. It is worth being aware that transverse and longitudinal waves are not the only type of motions undertaken by a wave—water waves are neither transverse or longitudinal, as particles move in both the perpendicular and parallel direction.
Physical quantities of sound
- Pressure (p): All fluids, including air, have pressure. Pressure is created when the particles in air collide with each other and with their surroundings. Pressure is defined as the total force of these collisions per unit area. The pressure exerted by all of Earth's air upon the ground, or atmospheric pressure, is 101325 pascals. Sound, though, causes fluctuations in the pressure in some regions of air because of the bumping and vibrating of air molecules, so there may exist a pressure difference from atmospheric pressure. This pressure difference is called sound pressure or acoustic pressure. For example, if the atmospheric pressure is 101325 pascals, and the pressure of air in a specific place is 101325.1 pascals, the acoustic pressure is [math]\displaystyle{ 101325.1 - 101325 = 0.1\,\mathrm{Pa} }[/math]. If the acoustic pressure is zero, then there is no pressure difference, and the pressure is equal to atmospheric pressure.
- The maximum value of this pressure difference is known as the pressure amplitude. For example, if the acoustic pressure ranges from -2 mPa to 2 mPa, the pressure amplitude is 2 mPa.
- Displacement amplitude (A): The maximum value that any single particle is displaced in a sound wave. In other words, the displacement amplitude is the maximum amount that any of the air particles moves because of the sound wave. Maximum and minimum displacement always occur at points in the sound wave where the pressure difference (acoustic pressure) is zero because particles are densely packed together at regions of high pressure, so they are less capable of bumping past each other, and thus less capable of displacing.
- Power (P): Moving air particles have kinetic energy, so as a sound wave moves, it transports energy along with it. Power is how fast the sound wave carries this energy: more precisely, it is the amount of energy transported divided by the time it took. The concept of power is especially useful when talking about speakers because if you have a speaker, you will want to know how fast to transfer electrical energy into the speaker in order to be converted to sound energy (scientists also call sound energy "acoustic energy").
- Intensity (I): Power transmitted per area receiving energy; that is, [math]\displaystyle{ I=\frac{P}{A} }[/math]. Most of the time, you will use the formula [math]\displaystyle{ I=\frac{P}{4\pi r^2} }[/math] on sounds of music tests, where [math]\displaystyle{ r }[/math] is the distance away of an observer from the source. This equation results as a point source radiates sound uniformly in every direction, implying the energy is transmitted onto the surface area of a sphere. However, in the case of a directional source that only emits sound in front of it and none behind, the proper equation is [math]\displaystyle{ I=\frac{P}{2\pi r^2} }[/math], with a two in the denominator, as the sound only covers half a sphere of area. In reality, it is very rare to find a source that perfectly emits sound only in the direction covered by half a sphere. On tests, if you are in doubt, use the equation for a point source that radiates sound spherically and omnidirectionally.
- Speed: The speed of sound changes based upon medium. Sound is fastest in solids, then in liquids, and slowest in gases. Some equations for the speed of sound are given below.
- [math]\displaystyle{ v = \sqrt{\frac{B}{\rho}} }[/math] in a fluid with bulk modulus [math]\displaystyle{ B }[/math]
- [math]\displaystyle{ v = \sqrt{\frac{Y}{\rho}} }[/math] in a rod with Young's modulus [math]\displaystyle{ Y }[/math]
- [math]\displaystyle{ v = \sqrt{\frac{\gamma R\mathcal{T}}{m}} }[/math] in an ideal gas with adiabatic constant [math]\displaystyle{ \gamma }[/math], temperature [math]\displaystyle{ \mathcal T }[/math], and molar mass [math]\displaystyle{ m }[/math]
- [math]\displaystyle{ v = 20.05\sqrt{\mathcal T} }[/math] in air at temperature [math]\displaystyle{ \mathcal T }[/math] in Kelvin
Music production
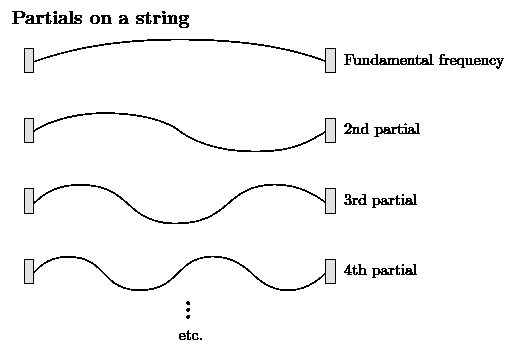
For musical instruments with a definite pitch, making music requires the capacity to generate a a pitch and sustain it long enough for the human brain to interpret it as potentially musical. All pitches are associated with a frequency, which the instrument must produce. Most instruments can produce a variety of frequencies for a single pitch. Often, but not always, the frequency you hear is the fundamental frequency, which is the lowest of the frequencies produced. The frequencies are higher than the fundamental, and so we accordingly call them overtones.
The frequencies at which standing waves can occur (i.e. overtones plus the fundamental) are collectively called partials. If all partials are integer multiples of the fundamental, we may also call them harmonics. The first harmonic is the same as the fundamental frequency. We denote the [math]\displaystyle{ n\text{th} }[/math] harmonic with [math]\displaystyle{ n }[/math], where [math]\displaystyle{ n=1 }[/math] is the fundamental frequency. The reason for overtones is that standing waves of different lengths can be fit onto a single musical instrument:
- Waves on a string of length [math]\displaystyle{ L }[/math] and linear mass density [math]\displaystyle{ \mu }[/math] under tension [math]\displaystyle{ T }[/math]
- [math]\displaystyle{ f_n = \frac{nv}{2L} = \frac{n}{2L}\sqrt{\frac{T}{\mu}} }[/math]
- Air column of a pipe with both ends open
- [math]\displaystyle{ f_n=\frac{nv}{2L} }[/math]
- Air column of a pipe with one end closed and one end open
- [math]\displaystyle{ f_n=\frac{nv}{4L} }[/math]
- Only odd [math]\displaystyle{ n }[/math] exist for such a pipe. In this case, the first harmonic would be n=1, followed by n=3, n=5, and so on.
We usually refer to pipes with both ends open as open pipes, and pipes with exactly one end closed as closed pipes.
Overtones, if present, are much like the fundamental in that they carry energy as they travel through the air into your air. When a band of overtones with close frequencies all carry a high energy, this high-energy region is known as a formant. Beyond instruments, formants are extremely important in speech production (this is intuitively reasonable as the human voice is a musical instrument, equipped with singing abilities). Indeed, you will be more likely to encounter the term "formant" in the acoustics of speech and singing than in the acoustics of non-voiced musical instruments. Moreover, instruments with "pure" tambres, such as clarinets, have few overtones, whereas an instrument like the bassoon would have an intricate overtone series.
Sound phenomena
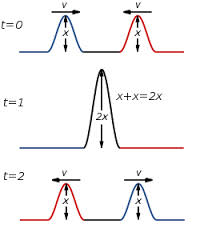
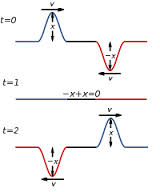
Interference/superposition - Sound waves, when encountering each other, will undergo interference. This means that at every point where both waves overlap, the pressure difference there will equal the sum of the pressure differences of the individual sound waves. Since it's as though we have added the waves on top of each other, we also call this the principle of superposition.
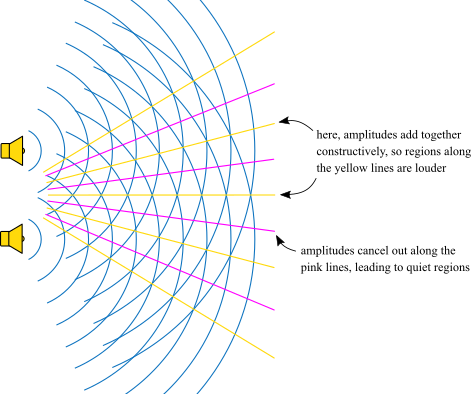
Two loudspeakers with the same input can serve as a demonstration of interference. When both loudspeakers are placed a distance of two or more meters apart and both play a single pure tone, the room will be filled with bands of loud regions and soft regions. Many classrooms today are arranged with such a system of two loudspeakers connected to a single computer, and if your Science Olympiad coach has such a classroom, you can ask them to help experimentally illustrate this effect. The outcome will resemble the image below.
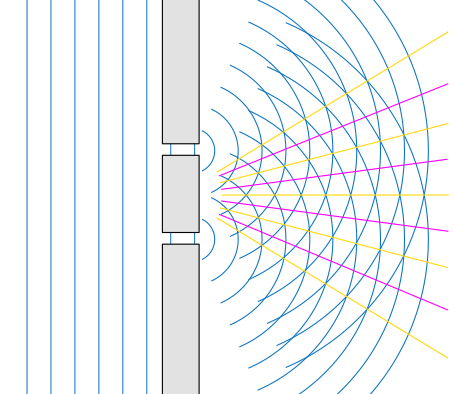
Diffraction - Diffraction is the phenomenon where waves spread around an object. It is partly diffraction in play when you hear sound despite being behind a wall, doorway, or other obstacle—the sound spreads out from an opening to diffract around the object, moving radially away from any boundaries.
Diffraction may be considered as a consequence or a special case of interference. Obstacles that block part but not all of a sound wave essentially convert the unabsorbed sound into one or more point source of sources of sound, which seem to emit sound waves radially and perhaps interfere with each other. Compare, for example, the diffraction of sound waves through two small slits with the interference of sound from two loudspeakers as shown earlier.
For those with experience in optics, this is an analogy of the Huygens-Fresnel principle for sound. It also explains why smaller openings result in sound waves spreading out over a wider angle. (Larger openings essentially act as many thin slits separated by infinitely small distance, while smaller openings act as fewer slits, also separated by zero distance.) Of this, Richard Feynman writes that
No-one has ever been able to define the difference between interference and diffraction satisfactorily. It is just a question of usage, and there is no specific, important physical difference between them. The best we can do is, roughly speaking, is to say that when there are only a few sources, say two, interfering, then the result is usually called interference, but if there is a large number of them [possibly infinite], it seems that the word diffraction is more often used.
Dispersion - In many media which we are accustomed to, sound only travels at one speed. This does not have to be the case, however. When waves of different frequencies travel at different speeds, this is called dispersion. Air is non-dispersive, but water and ice do cause dispersion of waves.
Doppler Effect - The Doppler effect occurs when a source of sound or an observer are moving relative to the sound. When this occurs, an observer may count a frequency different from the frequency emitted by the source of sound. A moving source, like the sirens of an ambulance, will inevitable get closer to some previously emitted wavelets and farther from others, leading to some waves bunching up and others spacing out. Observers will also "run into" wavelets of sound at a different rate if they are running towards or against the waves, and this too affects the frequency they measure. The frequency of a Doppler shift of sound is
- [math]\displaystyle{ \frac{f_\text{obs}}{f_\text{src}} = \frac{v + v_\text{obs}}{v + v_\text{src}} }[/math]
where [math]\displaystyle{ v }[/math] is the speed of sound, and the positive direction of [math]\displaystyle{ v_\text{src} }[/math] and [math]\displaystyle{ v_\text{obs} }[/math] is from the observer to the source. Unlike many phenomena of sound, the Doppler shift equation for sound is not true of all other types of waves.
Reflection - Reflection occurs when a wave encounters a boundary and as a result moves in the opposite direction. Reflection is responsible for both echoes and reverberation.
A common mistake made by students is to assume that only solid obstacles can cause reflection. While walls and other non-absorbent obstacles may be familiar to most of our everyday experiences, sound waves can reflect off of many sorts of boundaries. It is even possible for sound to travel into the upper atmosphere before reflecting back down to the ground.
Refraction - Refraction is the change in the direction of a sound when the speed of sound changes. Different media vary in their speed of sound, leading to refraction as sound enters from one material to another.
Resonance - An object or air column may vibrate at its fundamental frequency or an overtone when a force is applied to the object at certain frequencies. When the force is applied at other frequencies, the object or air does not vibrate with as much energy. This phenomenon is called resonance.
The Tacoma Narrows Bridge, located in the state of Washington, collapsed under conditions of high wind in 1940. While teachers and textbooks sometimes attribute the catastrophe to the bridge vibrating in step with the wind, thereby driving resonance, resonance most likely was not mainly responsible for the destruction of the bridge. Newer textbooks tend to identify this report as a misconception or at least contentious.
Music theory
It is a good idea for both partners to already have some background in music theory (for instance, from orchestra, band, or choir.). Competitors with background knowledge can easily skip much of the information in this article. Although the rule manual names several music theory topics to be within the scope of the written test in 4.c.v, the rules also allow questions to cover any "associated music terms" and all "fundamental elements of musical sound." This means a need for particularly detailed recall may arise on a test, since music theory encompasses broad swaths of knowledge, some of which is specific to only a few instruments. Fortunately, event supervisors mostly stick to beginner or moderate topics like those expressly identified in the rules, making the event more manageable.
Note names
Notes have letter names from A to G in order of pitch. They are arranged on a staff consisting of five bar lines. There are many, many notes, but only seven letter names from A to G, so letter names will begin to repeat after G. Notes with the same letter name are members of the same pitch class, and the interval separating consecutive members of a pitch class is known as an octave. We may subdivide the octave into twelve notes, each note situated a half step from the next. An interval of two half steps is called a whole step.
If there are seven letter names, why are there twelve half steps? Some notes exist between the others in pitch. We notate notes one half step above another with a sharp (♯) and those one half step below with a flat (♭). For example, the note one half step below E is E♭ (pronounced "E flat") or D♯ (because it is one half step above D). Why, then, are there not fourteen half steps (seven letter names plus sharps/flats)? Only one half step exists between B and C, and between E and F, meaning that B sharp is C, and C flat is B. We also employ the words "sharp" and "flat" to describe pitches that are higher and lower respectively relative to a reference note.
Scales and keys
By playing the notes C, D, E, F, G, A, B, and C, in that order, we create the major scale. In contrast, by playing A, B, C, D, E, F, G, and A, in that order, we create the natural minor scale, or more simply, the minor scale.
Observe that if every note of the major scale listed above is shifted by one half step up, then the result still sounds like a major scale. In fact, it is a major scale. The same happens if each note is shifted up by a whole step: it still sounds like a major scale (because it is a major scale). That we can shift all notes without changing the relative intervals between notes is due to a change in key. As switching key is essentially adding sharps and flats to every note of certain letter names, we write these sharps or flats beside the clef or a bar line, in what we call the key signature. We always use only flats or only sharps, and never mix both in the key signature.
The key of C has the only key signature with neither sharps nor flats.
Other scales exist, such as natural minor and harmonic minor scales. In addition, some tests will ask questions about various chords, cadences, and less common scales. It is thus useful to have a glossary of musical terms in your binder in case an obscure music theory question comes up.
Tempo
Tempo is the rate at which notes are played. Composers may recommend a tempo in beats per minute for a precise dictation for the speed of a musical piece, or they may simply write a short description for the overall sensation that listeners should feel upon hearing the piece. These descriptions are generally in either English or Italian. The most common tempo descriptors include the following.
- Largo: widely (i.e., slowly)
- Lento: slowly
- Moderato: moderate
- Allegro: fast
- Presto: very fast
Italian tempo indicators are always italicized. Because these are direct translations from Italian, the possible ways to describe tempo are only limited by the number of associated Italian words and phrases.
Additionally, composers use expressions like "accelerando" to indicate an increase in tempo (think accelerating) and ritardando to indicate a decrease in tempo. A glossary of tempo-related terms may also be useful for your notes.
Solfège
Solfège syllables are a group of systems that connect notes to a syllable. The syllables include do, re, mi, fa, sol, la, and ti. Solfège systems enjoy large popularity in formal choral education.
The two major subgroups of solfège systems are fixed do solfège and movable do solfège. Fixed do solfège is rarely used within the English-speaking world. In fixed do solfège syllables, each syllable corresponds to a pitch class. This typically means that do refers to C, re refers to D, mi refers to E, and so forth.
Movable do solfège is used mainly in the Anglophone world, and your event supervisor is more likely to be familiar with a movable do solfège system. Indeed, in the United States, use of the word solfège typically implies moving do solfège. In a movable do system, the first note in a major scale is assigned to do; the second is assigned to re; the third is assigned to mi, and so forth, until do is reached again. For a minor scale, a musician would begin with la for the first note, then ti for the second, then do, and so on. Movable do solfège can flexibly account for any major or minor scale, as any tone can be designated as do, and all other syllables will follow the same order as they would follow in any other key.
Musicians have modified solfège systems in a multitude of ways to adjust the system to serve their pedagogic practices. For instance, there exist multiple modified solfège systems that extend syllables to all 12 notes in an octave, rather than just the 8 in a major scale.
Each solfège syllable also corresponds to a certain hand sign. Instructors sometimes encourage students to sing a syllable simultaneously with a hand sign to help students to sing.
Psychology
Pitch is the human perception of frequency. Our ears are tuned to hear frequencies from approximately 20 Hz to 20000 Hz, but not all frequencies are treated equally to our ears. The distance between two notes in pitch is (approximately) determined by the ratio of their pitches, so a 100 Hz and 120 Hz note seem to be the same interval apart as a 1000 and 1200 Hz note. Meanwhile, an increase from 1000 Hz to 1020 Hz would seem tiny in terms of pitch, and few might notice the difference. In the special case that one note has twice the pitch of another, both notes may sound "the same" with respect to all other notes, except that one of the two notes sounds higher. This interval is defined as an octave.
Loudness is the human perception of intensity. Like pitch, the relative loudness of two sounds depends on the ratio of the intensities, although loudness is more subjective. Two musicians are more likely to disagree about how loud a note is compared to a reference note, and less likely to disagree about the pitch difference between two notes.
Beyond sound, perception in ratios is actually common in the human experience. Blindfolded, you could probably easily feel the weight difference between a 50 gram and 100 gram laboratory mass, but masses of 10.050 kilogram and 10.1000 kilograms would feel equally exhausting to hold aloft. Scientists Ernst Weber and Gustav Fechner are credited for first methodically recording this effect.
Linguistics
Linguistics is the scientific study of language. In the event that linguistics appears on a sounds of music test, it will almost exclusively be in the form of phonetics.
Amusia is the inability to process music. Intriguingly, amusia is not necessarily implied by aphasia, which is the inability to produce or understand language.
The Instrument
Half of the fun of Sounds of Music is building an instrument. You will need to build one durable, original, and creative instrument with which you will play a scale and a short song. You will also need to answer questions about the theory of your instrument and how you built it.
Building an Instrument
For 2019 and 2020, participants are required to build one instrument of any type, barring electrophones. The instrument must be played in such a way that all energy put into the instrument to make a sound must originate from the team. This differs from rules prior to the 2019 season, which had competitors building two instruments.
No commercially available instrument parts are allowed, (i.e. mouthpieces, mallets) excepting strings. Experiment with different materials. PVC pipe is a common material that is cheap and easy to make into an instrument; PVC pipe aerophones are very common. Other instruments very commonly made include idiophones (xylophone, marimba, etc.). Try different types of metal pipes and different types of wood to see what works best. There are several resources online that will provide an exact length to cut the bars to, but in order to achieve an exact pitch fine-tuning will likely be necessary.
When building an idiophone or other percussion instrument that is hit, it is important to consider the material with which the mallets will be built. If a soft material such as rubber or yarn is used, the percussion instrument could be drowned out by a wind instrument. If a harder material is used, the instrument will have a harder, clearer tone, but the tone quality may suffer. Once again, experimentation is key to determine what suits the instrument best.
Remember that the instrument MUST be in the allowable range. For the 2019-2020 season, the range of the instrument must be from F2 to F3. See this page for more about determining pitch.
There are four basic classifications of instruments under the Hornbostel-Sachs system as shown below. The fifth, electrophones, was not included for several years after the creation of the Hornbostel-Sachs system and is not used in competition.
Idiophones
An idiophone is an instrument in which the vibration of the instrument itself is what creates sound. They are generally the percussion instruments that are hit, shaken, or rubbed to create sound. Resonators can also be added to these instruments to create a sound.
In this event, the major type of idiophones created are xylophones, marimbas, or chimes. When you double the length of a bar, you cut the frequency in a fourth (put it down two active octaves). So in these instruments, to go down an increment of the scale, you must decrease the note length by a factor of the 24th root of 2. These also require you to fine-tune (sand/file).
Examples of idiophones include
- Xylophones
- Bells
- Steel Drums
- Wine Glasses
Membranophones
Membranophones are instruments that have a vibrating membrane over a resonator to create sound. These instruments are generally harder to build and perfect.
Examples of membranophones include
- Tuned drums
- Timpani
- Kazoo (Note for the 2018-2019 season, the rules do not allow for making an instrument that requires participants to sing or hum into it, thus a kazoo is not allowed.)
Aerophones
In aerophones, the sound is produced by a vibrating column of air within the instrument. The air is usually produced in one of two ways: the player directs wind towards a sharp edge, creating an oscillating wind going in and out of the pipe; or, the player buzzes his/her lips against a mouthpiece, creating a vibrating column of air that goes into the pipe. The wind that goes into the pipe vibrates, creating a sound wave. Pitch is changed by the changing size of the column of air.
Examples of aerophones include
- Flutes
- Pan Flutes
- Tubas
- Trombones
- Horns/Trumpets
Chordophones
In chordophones, the sound is produced by a vibrating string. The vibration of strings produces standing waves producing fundamental frequency as well as harmonics (the relative abundance of these make up the timbre of your instrument). Resonators added to the string will enhance the sound by vibrating sympathetically with them.
In chordophones, the wavelength made is twice the length of the string. Since we know that velocity equals frequency times wavelength, after assuming that the velocity of sound in the string will remain constant, we find that when one doubles length, frequency will be cut in half (note goes down an octave). Because the relationship between length and frequency is exponential we know that for every increment one goes up in a scale (1/12), the note increases by a factor of the 12th root of two. You can use this fact for starting your tuning. Unfortunately, you'll need some fine tuning and many hours to get your instrument to play accurate notes due to imperfections in string and to the fact that there will be different amount of tension on different strings (when playing different notes on single guitar string, there will be different amounts of tension). This will result in different velocities of sound in the string, making this form of tuning less reliable.
Examples of chordophones include
- Guitars
- Violins
- Harps
- Zithers
- Lyres
- Piano/Harpsichords (on the harder side to make, not advised)
Electrophones
NOTE: Electrophones are not allowed under the rules for 2013 and beyond.
Concerning electrophones, sound is produced by an electrically powered oscillator. It is highly unlikely anyone will build this type of instrument for Sounds of Music anytime in the near future, and it is also barred from competition under 2013 rules.
Examples of electrophones include
- Theremins
- Synthesizers
Past Rules
In 2019, Sounds of Music underwent significant event changes. The following section details the event structure under the old rules, for reference and in the event that the old structure returns in the future.
Past Rules
2018-19 seasonSounds of Music underwent a significant makeover from previous season. Participants were tasked with building a single instrument. The instrument was tasked with playing the pitches of a diatonic major scale as accurately as possible (pitch score test, 36 points) and with playing a pitch with as much intensity as possible up to a maximum of 85 dB SIL (volume score test, 9 points). Teams also took a written test (45 points) and created a log describing their instrument (10 points). Unlike the 2019-20 season, there was no minimum error in frequency on the pitch score test. In the most competitive tournaments, this led to many teams' pitch scores falling within mere fractions of a point, as top teams had nearly perfect pitch accuracy. Pre-2019While much of the work for the Sounds of Music event takes place before the competition, in the form of building, tuning, and practicing, only one part actually counts for Science Olympiad, and that is the competition. The SetupWhen you arrive in the competition room, you will be at least 30 seconds, if not more, to set up. If you are ready in less than 30 seconds, you will receive a 5 point bonus. This normally isn't a problem, as most instruments are mounted or otherwise ready to play. Some teams do bring xylophones that are not mounted or otherwise connected, and these teams will likely use the majority of the time. The room will likely have very few resources. There will be music stands where you may place your music, but other than that there is not much you can count on. Some competitions may provide a table or desks to place xylophones on, but it may be smart to bring your own portable table just in case. During the setup time, introduce yourself to your judges. Provide information such as your name, your school name, the type of instruments you created, and the pieces you will be playing. Give the judges a score of the music you wrote at this time as well. The MusicThe required piece of music this year is the theme from the 2nd movement of Dvorak's New World Symphony. The basic melody, written in the key of C in treble clef, can found on the second page of the Sounds of Music rule sheet. You may alter this piece by transposing it to a key to fit your instrument but the instrument which plays the melody must play the same notes as provided on the rules, with no changes. You will also be expected to compose your own harmony to this piece, which the second instrument will play. The second piece of music is completely your own creation. You may play anything you wish, from classical to pop to simple tunes like Twinkle, Twinkle, Little Star. It is best to play a song the judge will recognize. As with the required piece, you will need to write out your music with melody and harmony. Concerning writing the music, there are a few requirements you must abide by. As mentioned before, the melody of the New World Symphony theme must be exactly what is written on the rules (though it may be in a different key). The music the higher instrument plays MUST be written in treble clef, and the music the lower instrument plays MUST be written in bass clef. Give the judges a copy of the music with both parts on the same page- you'll probably get it back later. Also make sure that your names, team name, and team number are on the music, since this is worth a couple points. It is a good idea to write the music with music notation software. It looks more professional and has been recommended by judges at several competitions. Music software also makes sheet music easier to read, rather than what you may write by hand, no matter how good your handwriting is. Some suggestions for music notation software are:
Technical InterviewThe final portion of the event is the technical interview. It may be oral or written. In this section, you will have to explain how you built your instruments and how they work. You will also need to explain the sound theory behind your instrument and some of the physics of sound. BOTH team members will need to participate in the interview to get full marks. The technical interview generally becomes more important as the year goes on (and the competition becomes tougher). This is because your opposition usually gets tougher as well and many more instruments sound 'real'. Because of this, the interview will become a huge separator of teams. Make sure you understand the physics of sound and wave theory, basics of resonance, basics of tempering, and go into as much depth as possible into how your own instruments function. Many people take this part of the competition lightly, but 30 points is nothing to scoff at. This website provides much of the knowledge needed for the technical interview portion. Rubric OverviewThe highest score possible for this event, according to the rules, is 100. 20 points are awarded for the building and choice of instruments, as well as tuning, 20 points are awarded for being able to play the required scale, as well as sound quality, 20 points are awarded for the performance, 20 points are awarded for the technical interview, and 20 points are awarded for correct music notation, playing in the correct range, and being ready to be judged within 30 seconds of walking into the room. |
Previous National Tournament Winners (Division C)
| Team | Bass Instrument | Treble Instrument | |
|---|---|---|---|
| 2007 | Troy High School | Guitar | Trumpet |
| 2008 | Valparaiso High School | Guitar | Xylophone |
| 2011 | Harriton High School | Marimba | Flute |
| 2012 | Camas High School | Marimba | Violin |
| 2020 | Solon High School | unknown | n/a |
| 2021 | West Windsor-Plainsboro High School South | unknown | n/a |
In the 2018-19 and 2019-20 seasons, each team required only one instrument in this event.
Instrument Instructions
Here are websites with tutorials to make instruments:
- Percussion