Codebusters
- This page contains a large number of equations and mathematical symbols, which may take some time to load.
| Codebusters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Type | Nature Of Science | |||||||
| Category | Lab | |||||||
| Description | Teams will cryptanalyze and decode encrypted messages using cryptanalysis techniques for historical and modern advanced ciphers. | |||||||
| Event Information | ||||||||
| Latest Appearance | 2023 | |||||||
| Forum Threads | ||||||||
| ||||||||
| Question Marathon Threads | ||||||||
| ||||||||
| Official Resources | ||||||||
| Website | www | |||||||
| Division B Results | ||||||||
| ||||||||
| Division C Results | ||||||||
| ||||||||
Codebusters is an event in Division C for the 2023 season and was held as trial event at both the 2016 National Tournament and the 2018 National Tournament. It was going to be held as a trial event for Division B at the 2020 National Tournament before its cancellation. In this event, up to 3 participants must decode encrypted messages, or they may be required to encode messages with certain advanced ciphers. Competitors are not allowed to bring any resources to this event, but can bring a 4 or 5 function calculator - no scientific or graphing calculators allowed.
Test Format
Format and Scoring
Tests are composed of a variety of questions where teams will encrypt or decrypt various code types. The number of questions on a given test is variable, but tests often contain anywhere from 6-24 questions, depending on the difficulty of the questions. The first question of a test is timed, and a time bonus is given for the question based on how quickly it is completed. Points may be deducted from questions based on the number of mistakes found in the answer given. If the answer differs from the solution by only one or two letters, then no points are removed, despite the answer having errors. Each additional error after two errors will result in a deduction of 100 points. The number of points removed from a question through deductions will not exceed the value of the question (meaning that deductions will never result in a question score below 0).
The First Question
The very first question is timed - when solved, a team member should signal the event supervisor that they have finished the question, such as raising their hand, shouting "bingo!", or another method determined by the supervisor before the event begins. The first question will be an Aristocrat with or without a hint. Teams will receive bonus points depending on their time, and they may make as many attempts as they want to break the code without any penalties. The timing bonus will be calculated from the start of the event until the question is answered successfully, or until 10 minutes have elapsed, and is calculated with the formula: 4*(600-number of seconds taken). Teams may still answer the question after 10 minutes; however, the timing bonus is 0. The first cryptogram may also be used as a tiebreaker. Solutions are given full points only if the solution is an exact match or differs by only one or two letters. Deductions for inconsistencies in the answer to the first question are treated the same as deductions for a non-timed question.
Question Point Distribution
The amount of points each question is worth will be distributed by the following:
- An easy question: 100-150 points
- A medium question: 200-300 points
- A hard question: 350-500 points
- A very hard question: 550-700 points
In the case of a tie, select questions predetermined by the event supervisor will serve as a tiebreaker. The tie is broken using the following criteria in this order: score, degree of correctness, and number attempted.
Code types that may be used at the Invitational and Regional Competitions
- Atbash Cipher
- Caesar Cipher (shift cipher)
- Mono-alphabetic substitution (can use K1, K2, or random alphabets)
- Aristocrats with a hint, spaces, and no spelling errors - messages with spaces included, and with a hint
- Aristocrats with no hint, spaces, and no spelling errors - messages with spaces included, but without a hint
- Aristocrats with a hint, spaces, and spelling errors- messages with spaces and hints, but including spelling/grammar errors
- Aristocrats with no hint, spaces, and spelling errors- messages with spaces and including spelling/grammar errors but no hints
- Patristocrats with a hint - messages with spaces removed, and with a hint
- Patristocrats without a hint - messages with spaces removed, but without a hint
- Affine Cipher - encryption and decryption
- Vigenère Cipher - encryption/decryption only, not cryptanalysis
- Baconian Cipher and its variants
- Xenocrypt (no more than one)
- Mathematical Cryptanalysis of the Hill Cipher - either producing a decryption matrix given a 2x2 encryption matrix or computing a decryption matrix given 4 plaintext-ciphertext letter pairs.
- Pollux and Morbit Ciphers - decrypting Morse code ciphertext encoded as digits and spaces given the mapping of at least 6 of the digits
Code types that may be used at the State and National Competitions
- All Invitational and Regional code types
- Running Key Cipher
- Cryptanalysis of the Vigenère cipher with a 'crib' (a known plaintext attack)
- RSA Cipher
- The Hill Cipher - encrypting or decryption with a provided 2x2 or 3x3 matrix.
- Xenocrypt - at least one cryptogram will be in spanish
- Mathematical Cryptanalysis of the Affine Cipher
Code Types
Atbash Cipher
The Atbash Cipher is a variant of the affine cipher (see above) in which both a and b equal 25. This results in the alphabet essentially becoming a mirror (A corresponds to Z, B corresponds to Y, C corresponds to X, etc.).
| Original Alphabet | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ciphertext Alphabet | Z | Y | X | W | V | U | T | S | R | Q | P | O | N | M | L | K | J | I | H | G | F | E | D | C | B | A |
Following the affine cipher, the encryption formula would be:
[math]\displaystyle{ E(x) = (25x + 25) \mod 26 }[/math]
However, observing the mirror like alphabet yields a much simpler equation of:
[math]\displaystyle{ E(x) = D(x) = 25 - x }[/math]
Since the alphabet is like a mirror, encryption is the same as decryption.
Encryption Example
Encode "encrypt" with the Atbash Cipher.
| Plaintext | E | N | C | R | Y | P | T |
|---|---|---|---|---|---|---|---|
| Numeric Component | 4 | 13 | 2 | 17 | 24 | 15 | 19 |
| [math]\displaystyle{ 25 - x }[/math] | 21 | 12 | 23 | 8 | 1 | 10 | 6 |
| Ciphertext | V | M | X | I | B | K | G |
The cipher text is "vmxibkg."
Decryption Example
Decode "zmhdvi" with the Atbash Cipher.
| Plaintext | Z | M | H | D | V | I |
|---|---|---|---|---|---|---|
| Numeric Component | 25 | 12 | 7 | 3 | 21 | 8 |
| [math]\displaystyle{ 25 - x }[/math] | 0 | 13 | 18 | 22 | 4 | 17 |
| Ciphertext | A | N | S | W | E | R |
The plaintext is "answer."
Caesar Cipher
One example of a mono-alphabetic substitution is Caesar shift cipher, where each letter is replaced by one shifted by a certain amount. For example, the following table has each letter shifted three positions to the right.
| Original Alphabet | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shifted Alphabet (to the right 3) | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
From this table, it is clear that each shifted letter is the same as the original letter three spaces from it (A becomes D, B becomes E, etc). Thus, a message like "Science Olympiad is cool" would become "Vflhqfh Robpsldg lv frro" using a Caesar shift of 3. The alphabet can be shifted any number of times. This type of cryptogram can be solved through brute force, by taking a section of the message and writing out all 26 possible shifts below it, upon which the message is easily revealed.
Encryption Example
Encode "example" with a shift of 7.
By shifting each letter 7 times, we can encrypt the text.
| Encryption Shift | Possible Plaintext |
|---|---|
| 0 | example |
| 1 | fybnqmf |
| 2 | gzcorng |
| 3 | hadpsoh |
| 4 | ibeqtpi |
| 5 | jcfruqj |
| 6 | kdgsvrk |
| 7 | lehtwsl |
The encrypted text is lehtwsl.
Decryption Example
Decode "xhntqd".
We must test all possible shifts of our text to solve this prompt, since we do not know the shift. By repeatedly testing different shifts, we will eventually arrive at our answer.
| Decryption Shift | Possible Plaintext |
|---|---|
| 0 | xhntqd |
| 1 | wgmspc |
| 2 | vflrob |
| 3 | uekqna |
| 4 | tdjpmz |
| 5 | scioly |
After shifting "xhntqd" five times, the plaintext is revealed to be scioly, and no further shifts need to be tested.
Mono-alphabetic Substitution
A mono-alphabetic substitution is one where the same plaintext letters are replaced by the same ciphertext letters. Since specific encryption/decryption methods are not mentioned in the rules, a variety of ways will be covered in the following section. Mono-alphabetic ciphers may contain spaces (Aristocrats) or may have spaces removed (Patristocrats). Mono-alphabetic ciphers may use K1, K2, or random alphabets as defined by the ACA.
Solving a mono-alphabetic substitution cipher using patterns
This may be the most common way to solve a cipher on a Code Busters test, because the supervisor may not write that a Caesar cipher etc. was used to encrypt.
First, find the corresponding letter for a few cipher letter by:
- Look for words that are only one letter long. These will almost always be A or I, unless the cryptogram is a poem, in which case O may be used. I usually appears at the start of the sentence, while A is usually more common.
- Look for repeated blocks of three. The block is often THE: THE is the most common english word, used almost twice as often as the second most common, BE.
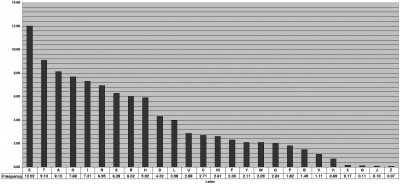
- Look for frequency of letters. The 12 most frequent letters in the English alphabet are ETAOIN SHRDLU, with E being the most common by a significant margin.
- Look for contractions. If an apostrophe is seen in the ciphertext, it can be an easy way to start deciphering using the table below.
- Look for double letters. They're often LL, followed in frequency by EE, SS, OO and TT.
Two clues may give different substitution, in which case experimenting may be helpful.
Then, substitute the known letters, and gradually decode more words using the word fragments. Starting with two or three-letter words are often easier, because of the limited possibilities.
| Endings | Examples |
|---|---|
| 'T | Aren't, Can't, Couldn't, Didn't, Don't, Isn't, Shouldn't, Weren't, Won't |
| 'S | It's, He's, She's, That's, There's, Who's |
| 'D | I'd, He'd, She'd, They'd, We'd, You'd |
| 'M | I'm |
| 'RE | They're, We're, You're |
| 'VE | They've, We've, You've |
| 'LL | I'll, It'll, He'll, She'll, They'll, We'll, Who'll |
Common word patterns include
- axx- all or too
- xaxb- away, even, ever
- xa xb- it is (at the beginning of questions, is it)
- xax... at the beginning of a word is probably eve(ry)
- ...xxa at the end of a word is possibly lly
- axbycxy- science
- abxcx- there (most common) where or these
- xabx- that (most common) high or dead
- axbcx- which
- xyaxby- people
- xayybxx- success (abcddxxyxy- succeeded).
(Note: a, b, c, x, and y are substitutes for real words)
Keep in mind less common words may occupy these frequencies. For example xyaxby could be "indian" instead of people. (But people is used more often)
Messages with Spaces and a Hint
These cryptograms are similar to those published in 20th century newspapers. These are usually solved using patterns, as described above, with the hint providing additional information to assist the decryption.
Messages with Spaces
These cryptograms are similar to NSA and diplomatic messages, and do not have a hint. These are usually solved using patterns, as described above.
Messages with Spaces and Spelling Errors
These cryptograms are similar to FBI and organized crime messages. These are often solved by patterns, with additional care:
- The letter frequencies likely do not change, and can be applied.
- THE and many of the most common words are seldom misspelled, unless intentionally. OF may be unintentionally misspelled as UV.
- Piecing together words with word fragments may be more difficult. Misspelled words often sound the same as the actual word, which can be used to check the decrypted message.
Messages without Spaces
These cryptograms are similar to NSA and espionage messages, and have a hint. An example is: "UVYNYGUSZYSBZBULAPIAZUACAZZAMLGFALPERAJZNYGUUAFBR". Students are told that the last word is TODAY, and the cipher begins with a three-letter word, followed by a four-letter word.
- Begin by writing in TODAY. UVYNYGUSZYSBZBULAPIAZUACAZZAMLGFALPERAJZNYGUTODAY. From this, we can see that U represents T, A represents O, F represents D, B represents A, and R represents Y.
- Replace the cipher text with the decrypted letters. TVYNYGTSZYSBZATLOPIOZTOCOZZOMLGDOLPEYOJZNYGTTODAY
- The first word is a 3 letter word beginning with T, which we can guess decrypts to THE. Replace Vs with H and Y with E. THENEGTSZESAZATLOPIOZTOCOZZOMLGDOLPEYOJZNEGTTODAY
- In this cipher, we can see the phrase "TOCOZZOM". Because of the double Z in the middle, it can be inferred that this decrypts to TOMORROW. Replace Z with R, C with M, and M with W. THENEGTSRESARATLOPIORTOMORROWLGDOLPEYOJRNEGTTODAY.
- We can see the letters YOJR. This is probably YOUR. Replace J with U. THENEGTSRESARATLOPIORTOMORROWLGDOLPEYOURNEGTTODAY.
- The letters LG after the noun TOMORROW likely decrypt to IS. Replace L with I and G with S. THENESTSRESARATIOPIORTOMORROWISDOIPEYOURNESTTODAY.
- NEST probably decrypts to B, as that is the only word that makes sense in this context. THEBESTSRESARATIOPIORTOMORROWISDOIPEYOURBESTTODAY.
- At this point, the cipher is able to be solved using common sense. SRESARATIOP likely means PREPARATION. IOR probably means FOR. DOIPE probably means DOING. Thus, the message is THE BEST PREPARATION FOR TOMORROW IS DOING YOUR BEST TODAY.
Messages without Spaces or Hints
These cryptograms are extremely difficult and may not be tested very frequently. In the event that a test does contain one, the best method is using the patterns listed above, especially finding repeated three letter "phrases" or double letters.
Affine Cipher and Modular Arithmetic
The Affine cipher uses an alphabet of size [math]\displaystyle{ m }[/math] with keys [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] such that [math]\displaystyle{ a,b }[/math] are integers, and [math]\displaystyle{ a }[/math] and [math]\displaystyle{ m }[/math] are coprime (there is no positive divisor for both of them besides 1). Assuming the alphabet is of size 26, [math]\displaystyle{ a }[/math] can be 1, 3, 5, 7, 9, 11 ,15, 17, 19, 21, 23 and 25. Each letter in the alphabet corresponds to a number from [math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ m-1 }[/math]. The most common correspondence for the English alphabet is shown below.
| Letter | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
The encryption formula for an Affine cipher is:
[math]\displaystyle{ E(x)=(ax+b)\bmod m. }[/math]
In the formula, [math]\displaystyle{ x }[/math] is the corresponding number of plaintext. For example, if encrypting N, [math]\displaystyle{ x }[/math] would be 13. Essentially, numbers are plugged into the formula and the resulting number corresponds to the encrypted letter.
For this example, we encode the message CODEBUSTERS using [math]\displaystyle{ a=9 }[/math] and [math]\displaystyle{ b=42 }[/math]. To slightly speed up the process, use the fact from modular arithmetic that the function [math]\displaystyle{ ax+b }[/math] does not change if we also take [math]\displaystyle{ a, b }[/math] modulo 26: the function [math]\displaystyle{ 9x+42 }[/math] is equivalent to the function [math]\displaystyle{ 9x+16 }[/math] or [math]\displaystyle{ 9x-10 }[/math].
| Plaintext | C | O | D | E | B | U | S | T | E | R | S |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ x }[/math] | 2 | 14 | 3 | 4 | 1 | 20 | 18 | 19 | 4 | 17 | 18 |
| [math]\displaystyle{ 9x+42 }[/math] | 60 | 168 | 69 | 78 | 51 | 222 | 204 | 213 | 78 | 195 | 204 |
| [math]\displaystyle{ (9x+42)\bmod 26 }[/math] | 8 | 12 | 17 | 0 | 25 | 14 | 22 | 5 | 0 | 13 | 22 |
| Ciphertext | I | M | R | A | Z | O | W | F | A | N | W |
The encrypted message is IMRAZOWFANW.
To decrypt the message given the key, use the decryption formula:
[math]\displaystyle{ D(x)=a^{-1}(x-b)\bmod 26 }[/math]
In this case, [math]\displaystyle{ a^{-1} }[/math] is the multiplicative inverse of [math]\displaystyle{ a }[/math] modulo [math]\displaystyle{ m }[/math] ([math]\displaystyle{ aa^{-1}\bmod m=1 }[/math]). Because there are only 26 values, one can brute force it to find the value of [math]\displaystyle{ t }[/math] where [math]\displaystyle{ ta \bmod m=1 }[/math]. [math]\displaystyle{ t }[/math] represents [math]\displaystyle{ a^{-1} }[/math].
| [math]\displaystyle{ t }[/math] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ 9t \bmod 26 }[/math] | 9 | 18 | 1 | 10 | 19 | 2 | 11 | 20 | 3 | 12 | 21 | 4 | 13 | 22 | 5 | 12 | 14 | 23 | 6 | 15 | 24 | 7 | 16 | 25 | 8 | 17 |
The table reveals that [math]\displaystyle{ a^{-1}=3 }[/math]. Below is a table of [math]\displaystyle{ a^{-1} }[/math] for [math]\displaystyle{ m=26 }[/math]:
| [math]\displaystyle{ a }[/math] | 1 | 3 | 5 | 7 | 9 | 11 | 15 | 17 | 19 | 21 | 23 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ a^{-1} }[/math] | 1 | 9 | 21 | 15 | 3 | 19 | 7 | 23 | 11 | 5 | 17 | 25 |
Decrypting then becomes a task of plugging into the formula.
| Ciphertext | I | M | R | A | Z | O | W | F | A | N | W |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ x }[/math] | 8 | 12 | 17 | 0 | 25 | 14 | 22 | 5 | 0 | 13 | 22 |
| [math]\displaystyle{ 3(x-42) }[/math] | -102 | -90 | -75 | -126 | -51 | -84 | -60 | -111 | -126 | -87 | -60 |
| [math]\displaystyle{ 3(x-42) \bmod 26 }[/math] | 2 | 14 | 3 | 4 | 1 | 20 | 18 | 19 | 4 | 17 | 18 |
| Plaintext | C | O | D | E | B | U | S | T | E | R | S |
Sometimes, some characters are given, which makes decryption much easier. For example, one might be given the ciphertext "CXWZ ZRC OWGW" and told that the first word is "EDIT". Thus, the characters are mapped as:
| Plaintext | Ciphertext |
|---|---|
| E (4) | C (2) |
| D(3) | X (23) |
| I (8) | W (22) |
| T (19) | Z (25) |
Write out two equations using the first two values and the equation [math]\displaystyle{ Output=ax+b \bmod 26 }[/math] in order to solve for [math]\displaystyle{ b }[/math].
[math]\displaystyle{ a\cdot4+b\bmod 26=2 }[/math]
[math]\displaystyle{ a\cdot3+b\bmod 26=23 }[/math]
Cancel out the [math]\displaystyle{ a }[/math] by multiplying to get the same value (same process as solving a system of equations).
[math]\displaystyle{ 12a+3b\bmod 26=6 }[/math]
[math]\displaystyle{ 12a+4b\bmod 26=92 }[/math]
Subtract the equations.
[math]\displaystyle{ b\bmod 26=86 }[/math]
Take the mod of the right side.
[math]\displaystyle{ b\bmod 26=8 }[/math]
Compute the modulus values to see which works. In this case, 8 works. Now, substitute [math]\displaystyle{ b }[/math] into the equation and repeat the process.
[math]\displaystyle{ a\cdot3+8\bmod 26=23 }[/math]
[math]\displaystyle{ a\cdot3\bmod 26=15 }[/math]
[math]\displaystyle{ a=5 }[/math]
Alternatively, you can also solve by cancelling out the b's.
[math]\displaystyle{ 4a+b=2(\bmod 26) }[/math]
[math]\displaystyle{ 3a+b=23(\bmod 26) }[/math]
Subtract the two equations and eliminate the b.
[math]\displaystyle{ a=-21(\bmod 26) }[/math]
Now add 26 (or 0 mod 26):
[math]\displaystyle{ \boxed{a=5} }[/math]
To solve for b, plug it back into one of the equation:
[math]\displaystyle{ 5\cdot4+b=2(\bmod 26) }[/math]
[math]\displaystyle{ 20+b=2(\bmod 26) }[/math]
[math]\displaystyle{ b=-18(\bmod 26) }[/math]
[math]\displaystyle{ \boxed{b=8} }[/math]
Vigenère Cipher
The Vigenère cipher, invented by Blaise de Vigenère in the 16th century, is a polyalphabetic cipher (this means that it is a substitution cipher but uses multiple substitution alphabets, so if A decrypts to B at some point, it does not necessarily mean that all of the A's will decrypt to B). This means that each letter is shifted by a different amount. According to the rules, students will probably be asked to encrypt rather than decrypt Vigenère ciphers. Encrypting is a fairly straightforward procedure.
Encryption/Decryption With a Table
First, write out the message with the key under it, repeating the key as many times as necessary. An example is shown.
| Message | S | C | I | E | N | C | E | O | L | Y | M | P | I | A | D | I | S | C | O | O | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Key | S | C | I | O | L | Y | S | C | I | O | L | Y | S | C | I | O | L | Y | S | C | I |
Then, take out the alphabet square, as shown below. This will typically be provided on the test.
Using the alphabet square, encode the plaintext. The first message letter is S and the first key letter is S, therefore, look at the table to see where row S and column S intersect. It is clear that they intersect at K, so write down K as the first letter of the ciphertext. Repeat this with the rest of the message. Thus, the encrypted text is "KEQSYAW QTMXNACL WD AGQT"
If the key and ciphertext are both given, decoding is also possible. This is done by taking a letter of the key and finding its row, finding the corresponding letter of ciphertext in that row, and seeing what column that letter falls in. The letter in the column is the letter of the plaintext. In the previous example, the first letter is decoded by going to row S and finding K, which is located in column S. Thus, the plaintext letter is S.
Encryption/Decryption Without a Table
Tables are typically given on the test, but in the event they are not, the following strategy may be more helpful.
Remember or recreate the correspondence between letter and number like in Affine and Hill Cipher, with A being 0 and Z being 25. Then, for each letter, convert the plain text and key to a sequence of numbers, and add the numbers modulo 26. Then, convert the number back to letter.
For example, if we encode the message "SCIENCEOLYMPIADISCOOL" using the key SCIOLY, we get
To decode a message using this method, subtract instead of add the key's corresponding number: The cipher text K with the corresponding key letter S gives plain text [math]\displaystyle{ 10-18=-8\equiv18\pmod{26}\to \text{S} }[/math].
Baconian Cipher
The Baconian cipher replaces each letter of the plaintext with a 5 letter combination of 'A' and 'B'. This replacement is a binary form of encoding, in which 'A' may be considered as 0 and 'B' as 1. One variant of the Baconian Cipher uses a 24 letter alphabet with the letters 'I' and 'J' having the same code, as well as 'U' and 'V'.
| Letter | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | aaaaa | aaaab | aaaba | aaabb | aabaa | aabab | aabba | aabbb | abaaa | abaaa | abaab | ababa | ababb | abbaa | abbab | abbba | abbbb | baaaa | baaab | baaba | baabb | baabb | babaa | babab | babba | babbb |
| Binary | 00000 | 00001 | 00010 | 00011 | 00100 | 00101 | 00110 | 00111 | 01000 | 01000 | 01001 | 01010 | 01011 | 01100 | 01101 | 01110 | 01111 | 10000 | 10001 | 10010 | 10011 | 10011 | 10100 | 10101 | 10110 | 10111 |
Another variant of this cipher uses a unique code for each letter (26 letter alphabet). However, in a rule clarification, only the 24 letter variation is to be used on Codebusters tests for the 2019 season.
| Letter | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | aaaaa | aaaab | aaaba | aaabb | aabaa | aabab | aabba | aabbb | abaaa | abaab | ababa | ababb | abbaa | abbab | abbba | abbbb | baaaa | baaab | baaba | baabb | babaa | babab | babba | babbb | bbaaa | bbaab |
| Binary | 00000 | 00001 | 00010 | 00011 | 00100 | 00101 | 00110 | 00111 | 01000 | 01001 | 01010 | 01011 | 01100 | 01101 | 01110 | 01111 | 10000 | 10001 | 10010 | 10011 | 10100 | 10101 | 10110 | 10111 | 11000 | 11001 |
Standard numbering systems use a base 10 method of counting (ones place, tens place, hundreds place, etc). What this means is that normally for example 24 = (2*10 + 4*1). The Baconian Cipher uses a base 2 system. The following is an example of base 2 converted to standard base 10: 01001 (base 2) = (0*16 + 1*8 + 0*4 + 0*2 + 1*1) = (1*8 + 1*1) = 9 (base 10). As seen in the chart above, 01001 corresponds to J, which is the 9th letter in the alphabet (assuming A = 0). When the first variant is shown, the numbering system will be off by 1 from J to U and off by 2 from V to Z. For example, 10100 = W, even though 10100 = 20 (base 10) which corresponds to U on the alphabet chart when A = 0.
When solving a question encoded with the Baconian Cipher, it is very likely that they won't explicitly give you "A" and "B" to use to find the corresponding letters. Most of the time, they'll have certain symbols or letters that are meant to represent "A" and "B". One example of this would be using all of of the even letters in the alphabet to represent "A" while all the odd letters represent "B". There are many different variants of this, including symbols on a keyboard and vowel/consonants. To solve a Baconian, try to group the different symbols/letters into two groups based on their properties, and assign one group "A" and the other group "B". If it doesn't work the first time, then switch the groups so that the previous "A" group is now the "B" group. If even then it doesn't seem to be working, then start over again and find a different characteristic to base the groups off of. For this reason, the Baconian Cipher can take longer than some of the other ciphers.
Xenocrypt
At the invitational/Regional level, one cryptogram may be in Spanish as a challenge. At the state level, there will be at least one. It may be helpful if one of the partners is fluent in or has a few years of knowledge in Spanish.
For Spanish cryptograms, n and ñ are treated as different letters. However, letters with accents are treated the same as without (a and á are the same). This means that, when working with cryptograms, accent marks do not factor in. Also, ch, ll, and rr are NOT considered distinct letters. Thus, "churro" would have 6 letters: c-h-u-r-r-o. The Spanish alphabet used for cryptograms is as follows:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z |
The frequency table of Spanish letters is as follows, from most to least frequent:
| Letter | E | A | O | S | N | R | I | L | U | D | T | C | M | P |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 14.08% | 12.16% | 9.20% | 7.20% | 6.83% | 6.41% | 5.98% | 5.24% | 4.69% | 4.67% | 4.60% | 3.87% | 3.08% | 2.89% |
| Letter | B | H | Q | Y | V | G | F | J | Z | Ñ | X | K | W | |
| Frequency | 1.49% | 1.18% | 1.11% | 1.09% | 1.05% | 1.00% | 0.69% | 0.52% | 0.47% | 0.17% | 0.14% | 0.11% | 0.04% |
Spanish cryptograms are often solved with patterns as well, with a few differences:
- Look for the two most common letters, instead of the most common letters: E and A have relatively close frequency, and are much higher than the rest.
- The most common spanish words are DE, LA, QUE, EL, EN. Since Spanish has far more two-letter words, it is helpful to decrypt them, using the placement of the letter E. QUE is the most common three-letter word, almost twice as common as the next ones.
- Decrypting words using word fragments are much more difficult for teams without fluency in Spanish.
Hill Cipher
NOTE: These cryptograms will be matrix based, and only use 2x2 or 3x3 matrices.
The alphabet for the Hill cipher has corresponding numbers as follows:
| Letter | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Encryption
Begin by picking a key matrix of either 2x2 or 3x3. These could be a 4 letter word or three 3 letter words. For this example, the key will be WIKI (2x2 matrix). Then, break the message into groups of two. This example will use the message SCIENCE OLYMPIAD, which would be split up into SC IE NC EO LY MP IA DZ. Notice that a Z is added in order to make the last group a group of two. Write the message and the key as matrices.
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} S \\ C \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 18 \\ 2 \end{pmatrix}=\begin{pmatrix} 412 \\ 196 \end{pmatrix}\bmod 26=\begin{pmatrix} 22 \\ 14 \end{pmatrix}=\begin{pmatrix} W \\ O \end{pmatrix} }[/math]
In the second step of the above equation, the matrices are multiplied. Although it may seem complicated, matrix multiplication is fairly straightforward.
[math]\displaystyle{ \begin{pmatrix} A & B \\ C & D \end{pmatrix}*\begin{pmatrix} E \\ F \end{pmatrix} }[/math]
The matrices are multiplied as follows: [math]\displaystyle{ A }[/math] and [math]\displaystyle{ E }[/math] are multiplied, then added to the product of [math]\displaystyle{ B }[/math] and [math]\displaystyle{ F }[/math]. [math]\displaystyle{ C }[/math] and [math]\displaystyle{ E }[/math] are multiplied and added to the product of [math]\displaystyle{ D }[/math] and [math]\displaystyle{ F }[/math]. Thus, the product of the matrices is:
[math]\displaystyle{ \begin{pmatrix} AE + BF \\ CE + DF \end{pmatrix} }[/math]
Matrix multiplication for 3x3 matrices is very similar.
[math]\displaystyle{ \begin{pmatrix} A & B & C \\ D & E & F \\ G & H & I \\ \end{pmatrix}*\begin{pmatrix} J & K & L \\ M & N & O \\ P & Q & R \\ \end{pmatrix} }[/math]
Just like in a 2x2 matrix, the row of the first matrix is multiplied by the column of the second matrix, giving the following product.
[math]\displaystyle{ \begin{pmatrix} AJ+BM+CP & AK+BN+CQ & AL+BO+CR \\ DJ+EM+FP & DK+EN+FQ & DL+EO+FR \\ GJ+HM+IP & GK+HN+IQ & GL+HO+IR \\ \end{pmatrix} }[/math]
It is important to note that in order to multiply matrices, the number of columns in the first matrix MUST equal the number of rows in the second matrix. The size of the product matrix is the number of rows in the first matrix x the number of columns in the second matrix.
The "mod" operation is also fairly straightforward. Essentially, it finds the remainder after dividing. For example, [math]\displaystyle{ 153 \bmod 26 }[/math] is equal to the remainder of [math]\displaystyle{ 153 / 26 }[/math], which is 23. On a scientific calculator, this is found by dividing the two numbers, subtracting the integer value from the answer, and multiplying the decimals by the number after "mod" (in this case, 26). Therefore, the process would be:
[math]\displaystyle{ 153/26=5.884615385 }[/math]
[math]\displaystyle{ 5.884615385-5=0.884615385 }[/math]
[math]\displaystyle{ 0.884615385*26=23 }[/math]
The rest of the encoding of the message is shown below.
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} S \\ C \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 18 \\ 2 \end{pmatrix}=\begin{pmatrix} 412 \\ 196 \end{pmatrix}\bmod 26=\begin{pmatrix} 22 \\ 14 \end{pmatrix}=\begin{pmatrix} W \\ O \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} I \\ E \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 8 \\ 4 \end{pmatrix}=\begin{pmatrix} 208 \\ 112 \end{pmatrix}\bmod 26=\begin{pmatrix} 0 \\ 8 \end{pmatrix}=\begin{pmatrix} A \\ I \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} N \\ C \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 13 \\ 2 \end{pmatrix}=\begin{pmatrix} 302 \\ 146 \end{pmatrix}\bmod 26=\begin{pmatrix} 16 \\ 16 \end{pmatrix}=\begin{pmatrix} Q \\ Q \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} E \\ O \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 4 \\ 14 \end{pmatrix}=\begin{pmatrix} 200 \\ 152 \end{pmatrix}\bmod 26=\begin{pmatrix} 18 \\ 22 \end{pmatrix}=\begin{pmatrix} S \\ W \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} L \\ Y \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 11 \\ 24 \end{pmatrix}=\begin{pmatrix} 434 \\ 302 \end{pmatrix}\bmod 26=\begin{pmatrix} 18 \\ 16 \end{pmatrix}=\begin{pmatrix} S \\ Q \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} M \\ P \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 12 \\ 15 \end{pmatrix}=\begin{pmatrix} 384 \\ 240 \end{pmatrix}\bmod 26=\begin{pmatrix} 20 \\ 6 \end{pmatrix}=\begin{pmatrix} U \\ G \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} I \\ A \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 8 \\ 0 \end{pmatrix}=\begin{pmatrix} 176 \\ 80 \end{pmatrix}\bmod 26=\begin{pmatrix} 20 \\ 2 \end{pmatrix}=\begin{pmatrix} U \\ C \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} W & I \\ K & I \end{pmatrix}*\begin{pmatrix} D \\ Z \end{pmatrix}=\begin{pmatrix} 22 & 8 \\ 10 & 8 \end{pmatrix}*\begin{pmatrix} 3 \\ 25 \end{pmatrix}=\begin{pmatrix} 226 \\ 230 \end{pmatrix}\bmod 26=\begin{pmatrix} 18 \\ 22 \end{pmatrix}=\begin{pmatrix} S \\ W \end{pmatrix} }[/math]
The encoded message is WOAIQQSWSQUGUCSW.
3x3 matrix encryption works in the same way. This example will encrypt "EDIT THE WIKI" using the key "BEE FLY BUG". First, split up the plaintext into groups of three, which becomes EDI TTH EWI KIZ. Once again, the last group has a Z added to make it a group of three.
[math]\displaystyle{ \begin{pmatrix} B & E & E \\ F & L & Y \\ B & U & G \end{pmatrix}*\begin{pmatrix} E \\ D \\ I \\ \end{pmatrix}=\begin{pmatrix} 1 & 4 & 4 \\ 5 & 11 & 24 \\ 1 & 20 & 6 \end{pmatrix}*\begin{pmatrix} 4 \\ 3 \\ 8 \end{pmatrix}=\begin{pmatrix} 48 \\ 245 \\ 112 \end{pmatrix}\bmod 26=\begin{pmatrix} 22 \\ 11 \\ 8 \end{pmatrix}=\begin{pmatrix} W \\ L \\ I \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} B & E & E \\ F & L & Y \\ B & U & G \end{pmatrix}*\begin{pmatrix} T \\ T \\ H \\ \end{pmatrix}=\begin{pmatrix} 1 & 4 & 4 \\ 5 & 11 & 24 \\ 1 & 20 & 6 \end{pmatrix}*\begin{pmatrix} 19 \\ 19 \\ 7 \end{pmatrix}=\begin{pmatrix} 123 \\ 472 \\ 441 \end{pmatrix}\bmod 26=\begin{pmatrix} 19 \\ 4 \\ 25 \end{pmatrix}=\begin{pmatrix} T \\ E \\ Z \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} B & E & E \\ F & L & Y \\ B & U & G \end{pmatrix}*\begin{pmatrix} E \\ W \\ I \\ \end{pmatrix}=\begin{pmatrix} 1 & 4 & 4 \\ 5 & 11 & 24 \\ 1 & 20 & 6 \end{pmatrix}*\begin{pmatrix} 4 \\ 22 \\ 8 \end{pmatrix}=\begin{pmatrix} 124 \\ 454 \\ 492 \end{pmatrix}\bmod 26=\begin{pmatrix} 20 \\ 12 \\ 24 \end{pmatrix}=\begin{pmatrix} U \\ M \\ Y \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} B & E & E \\ F & L & Y \\ B & U & G \end{pmatrix}*\begin{pmatrix} K \\ I \\ Z \\ \end{pmatrix}=\begin{pmatrix} 1 & 4 & 4 \\ 5 & 11 & 24 \\ 1 & 20 & 6 \end{pmatrix}*\begin{pmatrix} 10 \\ 8 \\ 25 \end{pmatrix}=\begin{pmatrix} 142 \\ 738 \\ 320 \end{pmatrix}\bmod 26=\begin{pmatrix} 12 \\ 10 \\ 8 \end{pmatrix}=\begin{pmatrix} M \\ K \\ I \end{pmatrix} }[/math]
The encoded message is WLITEZUMYMKI.
When given 4 corresponding plaintext and ciphertext letters, create two sets of equations and solve them. This can be done using using matrix methods (such as with Cramer's Rule) or with a system of equations (shown below).
For example if the plaintext ABCD corresponds to the ciphertext DCBA and you have to find the encryption key
[math]\displaystyle{ \begin{pmatrix} h & i \\ j & k \\ \end{pmatrix}, }[/math]
first create two plaintext matrices with AB and CD as such:
[math]\displaystyle{ \begin{pmatrix} 0\\ 1\\ \end{pmatrix}\ \text{and}\ \begin{pmatrix} 2\\ 3\\ \end{pmatrix}, }[/math]
as well as two ciphertext matrices with DCBA:
[math]\displaystyle{ \begin{pmatrix} 3\\ 2\\ \end{pmatrix}\ \text{and}\ \begin{pmatrix} 1\\ 0\\ \end{pmatrix}. }[/math]
Multiplying the key matrix by each plaintext matrix and setting the product equal to each ciphertext matrix, you get
[math]\displaystyle{ \begin{pmatrix} h & i \\ j & k \\ \end{pmatrix}\begin{pmatrix} 0\\ 1\\ \end{pmatrix}\ = \begin{pmatrix} 3\\ 2\\ \end{pmatrix} }[/math]
[math]\displaystyle{ \begin{pmatrix} h & i \\ j & k \\ \end{pmatrix} \begin{pmatrix} 2\\ 3\\ \end{pmatrix} = \begin{pmatrix} 1\\ 0\\ \end{pmatrix}, }[/math]
which can be multiplied out and written as systems of equations:
[math]\displaystyle{ 0h + 1i = i = 3 }[/math]
[math]\displaystyle{ 0j + 1k = k = 2 }[/math]
[math]\displaystyle{ 2h + 3i = 1 }[/math]
[math]\displaystyle{ 2j + 3k = 0. }[/math]
We can now substitute the values for [math]\displaystyle{ i }[/math] and [math]\displaystyle{ k }[/math] from the first two equations into the second two equations,
[math]\displaystyle{ 2h + 3(3) = 1 }[/math]
[math]\displaystyle{ 2j + 3(2) = 0. }[/math]
These equations can be solved to find that [math]\displaystyle{ h = -4\ mod\ 26 = -4 + 26 = 22 }[/math] and [math]\displaystyle{ j = -3\ mod\ 26 = -3 + 26 = 23 }[/math]. Now we have finally found our encryption key matrix:
[math]\displaystyle{ \begin{pmatrix} 22 & 3 \\ 23 & 2 \\ \end{pmatrix}, }[/math]
which can be verified by encrypting the plaintext using this key matrix and confirming that the result does indeed equal the ciphertext.
Decryption
The process for decryption is nearly identical to the process for encryption, with the only difference being that you are given the ciphertext and must multiply the letter groups by the decryption matrix to find the plaintext, instead of using the encryption matrix to find the ciphertext.
If the decryption matrix is given, you may skip to the multiplication step. If the encryption matrix [math]\displaystyle{ E }[/math] is given for a decryption problem, the following equation can be used to calculate the decryption matrix [math]\displaystyle{ D }[/math]:
[math]\displaystyle{ D = \left(\text{det}\ E\right)^{-1} \times \text{adj}\left(E\right), }[/math]
where [math]\displaystyle{ \left(\text{det}\ E\right)^{-1} }[/math] is the modular inverse of the determinant of the encryption matrix [math]\displaystyle{ E }[/math], and [math]\displaystyle{ \text{adj}\left(E\right) }[/math] is the encryption matrix's adjoint.
To illustrate with an example, begin with an encryption matrix:
[math]\displaystyle{ \begin{pmatrix} H & I \\ L & L \end{pmatrix} = \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} }[/math]
The determinant [math]\displaystyle{ \text{det}\ E }[/math] of a 2x2 matrix E can be found with the following formula:
[math]\displaystyle{ \text{det}\ E = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc\ \text{mod}\ 26 }[/math]
For the example matrix, the determinant is found to be 15:
[math]\displaystyle{ \text{det}\ E = \begin{vmatrix} 7 & 8 \\ 11 & 11 \end{vmatrix} = 7 \times 11 - 8 \times 11 = 77 - 88 = -11 = -11 + 26 = 15\ \text{mod}\ 26 }[/math]
When the determinant is negative, 26 must be added to make it positive when taking the modulo. The determinant is not always negative, but it must always be taken modulo 26.
The inverse determinant may be found in the modular inverses table of the reference sheet. This is one way in which the Hill inverse matrix differs from the typical inverse matrix - the modular inverse is taken instead of the multiplicative inverse. If the modular inverse does not exist (the determinant is not coprime with 26, as with the matrix used in the encryption example above), the key matrix is non-invertible and thus the ciphertext cannot be deterministically decrypted. In this example though, the modular inverse of the determinant exists and is 7.
Next, the adjoint is found using the following formula:
[math]\displaystyle{ \text{adj} \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} d & 26-b \\ 26-c & a \end{pmatrix} }[/math]
The typical adjoint formula does not include the 26 in front of the negated [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math], but these are included anyways since the modulo of each of the negative elements must be taken anyways. Representing the adjoint mod 26 this way can also make the calculation faster as it becomes a single step instead of negating the element and adding 26 each time.
For the example matrix, the adjoint is found to be:
[math]\displaystyle{ \text{adj}\left(E\right) = \text{adj} \begin{pmatrix} 7 & 8 \\ 11 & 11 \end{pmatrix} = \begin{pmatrix} 11 & 26-8 \\ 26-11 & 7 \end{pmatrix} = \begin{pmatrix} 11 & 18 \\ 15 & 7 \end{pmatrix} }[/math]
The decryption matrix can finally be calculated using the original equation:
[math]\displaystyle{ D = \left(\text{det}\ E\right)^{-1} \times \text{adj}\left(E\right) = 7 \times \begin{pmatrix} 11 & 18 \\ 15 & 7 \end{pmatrix} = \begin{pmatrix} 77 & 126 \\ 105 & 49 \end{pmatrix} = \begin{pmatrix} 25 & 22 \\ 1 & 23 \end{pmatrix} = \begin{pmatrix} Z & W \\ B & X \end{pmatrix} }[/math]
The decryption matrix has been found and the decryption "key" is ZWBX. Note that the final matrix should always be taken modulo 26.
If the cipher involves decryption using a 3x3 matrix, the decryption matrix should always be given. There does exist a process for calculating a 3x3 decryption matrix but it is unnecessary and thus left out for this reason.
Morse Ciphers
The Morse ciphers are a pair of ciphers where you are given a long text of numbers, where each number corresponds to one or two Morse characters (dot, dash, or a separator). Some of these number values will be given while some will not. Using the properties of Morse code and logical thinking, you must find the decryption for all of the missing numbers.
The dot and dash are self-explanatory. Separators, however, have two use cases:
- Letter separator: In this case, there will be one separator character (like an X) which separates two letters.
- Word separator: In this case, there will be two separator characters which separate two words.
There can never be more than two separator characters in a row. This is very useful when solving because it allows you to eliminate the possibility of a number next to two separators being another separator.
Pollux Cipher
In a Pollux cipher, each number corresponds to one Morse character. In a Pollux cipher (and only in a Pollux cipher), the quote cannot end with a separator.
An example question is given below.
Decode this quote which has been encoded using a Pollux Cipher, where 1 = x, 5 = x, 9 = x, 3 = •, 0 = •, 2 = -, and 7 = -.
086393425702417685963041456234908745360
First, you would replace the numbers you know already with their corresponding Morse characters.
•86• X •4- X -•-4 X -68 XX 6••4 X 4 X 6-•4 X •8-4 X •6•
Now, we turn our attention to the number 4 that is in between two X's. We know that this cannot be an X since that would put three X's in a row (which is illegal). This means it can only be a dash or a dot. In this scenario, you would look for another place where 4 is included, preferably with no other numbers and separators around it.
The text begins with "X •4- X -•-4 X". If we were to substitute a dot or dash in for the number 4, we would have two complete letters!. Substituting 4 for a dash would give "X •-- X -•-- X", which translates to "WY" (note that we ignore the "X"s since they are just separators and not actual letters). Although seeing "WY" is probably possible, it is very unlikely. Substituting 4 for a dot would give "X ••- X -•-• X", which translates to "UC". This is a much more probable combination, with many possible words such as "duck" or "luck".
Now, all 4's may be replaced with a •.
•86• X ••- X -•-• X -68 XX 6••• X • X 6-•• X •8-• X •6•
As entire Morse characters separated by X's appear, they can be replaced with their corresponding letter.
•86• X U X C X -68 XX 6••• X E X 6-•• X •8-• X •6•
At this point, you may chose to try finding out what the number 6 is, using the same process as with the number 4 using the four pieces separated by X's that only have a 6 in them (these are "6•••", "6-••", and "•6•"). However, one could also try to find out what the number 8 is. Since there aren't multiple pieces with only an 8 in them, this would be slightly more difficult.
Attempting to find out what the number 6 is, one may make a very keen observation by looking at the piece "6•••". Only the letter H ends with three dots so, since H starts with a dot, 6 must also be a dot.
A dot may now be substituted in for the number 6 and a few letters can be translated.
•8•• X U X C X -•8 XX H X E X L X •8-• X S
At this point, only the number 8 is missing. It cannot be X ("X -•8 XX" would break the rules of separators). At this point, any string can be looked at to solve the rest of the cipher. For this example, looking at the last piece with a number 8. This entire word reads, "HEL_S". One can often use guesswork at this point to deduce that the blank has to be a P to spell out "HELPS", but this can also be found systematically. The template is "•8-•", and it can be either "••-•" or "•--•", since the number 8 can only be a dot or a dash. If it were "••-•", then this word would be "HELFS", which doesn't make sense. Instead trying "•--•" gives the word "HELPS".
Now, 8 may be substituted in for a dash and the quote may finally be read fully:
L X U X C X K XX H X E X L X P X S
Luck helps! It is important to remember to ignore the X's that are separators, or else the quote will be unreadable. For this reason, it is advised to choose a non-alphabetic character, such as / or |, instead of an X to avoid confusion.
Morbit Cipher
In a Morbit cipher, each number corresponds to a pair of two Morse characters. Each pair of Morse character can only correspond to one number, meaning there are only nine possible decryptions. Whereas Pollux quotes cannot end with a separator, Morbit ciphers may or may not end with a separator. This is because each number has to correspond to two Morse characters, so an extra separator is added at the end if the quote in Morse code is an odd number of characters.
An example question is given below.
Decode this quote which has been encoded using a Pollux Cipher, where 5 = •-, 7 = -x, 1 = x•, 4 = -•, 8 = •x, and 2 = --.
27435881512827465679378
Begin by substituting what is given:
--- X -•3•-• X • XX ••- X •--• X --- X -•6•-6- X 93- X • X
Since the quote has an odd number of Morse characters, it ends with an X (separator) to make sure the last number corresponds to two Morse characters. Now, the complete Morse pieces can be translated into letters!
O X -•3•-• X E XX U X P X O X -•6•-6- X 93- X E X
It is important to remember here that X's are separators and not part of the quote. This quote does not contain any X's, but it is recommended that you use a different separator on an actual test so that you do not get confused if the quote does contain an X.
Here, we can apply a very important piece of knowledge about Morse code: No letter translates to more than four Morse characters (dots and dashes). Near the beginning, we see there is a piece that reads "X -•3•-• X". On the left of the number 3, we see two Morse characters, and on the right we see three. If the decryption of the number 3 did not contain an X, then this piece would be illegal because it would contain 2 + 2 + 3 = 7 Morse characters in a row.
To figure out what the number 3 decrypts to, we try substituting "X_" (separator followed by a blank that could be a dot or a dash) and "_X" (the first option but reversed). First trying "X_" gives "X -• X _•-• X", which translates to "N _", where the blank is another letter. This letter should look like "_•-•" in Morse. Using the constraints of the Morse alphabet, we know that the two letters that match this pattern are "••-•" (F) and "-•-•" (C). "NF" and "NC" are both reasonable, but we already know most of the first word, "O_E" (taking the two letters from the ciphertext above). This means it could either be "ONFE" or "ONCE", and it is clearly the latter, meaning that the number 3 is most likely "X-". Although there is the possibility of the number 3 being "_X", one could try this using the same strategy used above to see that it is probably not correct.
Now, substituting "X-" in for the number 3:
O X -• X -•-• X E XX U X P X O X -•6•-6- X 9 X -- X E X
Translating the new complete Morse pieces results in a few more known letters.
O X N X C X E XX U X P X O X -•6•-6- X 9 X M X E X
At this point, with very little left, one may often be able to guess what the remaining letters are without even working the Morse code out using basic decryption logic as with Aristocrats and Patristocrats. However, this example will continue using the Morse logic.
At this point, the numbers left are 6 and 9. Looking at the number 6 allows us to apply the same logic as with the number 3 using the fact that Morse letters are no longer than 4 characters. For sake of example, however, we take a look at the number 9. We see that it is a single number surrounded by X's, meaning it cannot contain an X. Since Morse code pairs (like ••, •-, •x, etc.) can only correspond to one number with Morbit ciphers, a table can be made of the known numbers and pairs.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| x• | -- | x- | -• | •- | ? | -x | •x | ? |
The only Morse code pairs missing are "XX" and "••"; however, it has already been established that the number 9 cannot contain an X, meaning it has to be "••". By process of elimination this means that the number 6 has to be "XX".
All the numbers are now known and the remaining ones can be substituted in for their Morse decryption.
O X N X C X E XX U X P X O X -• XX •- XX - X •• X M X E X
Converting the Morse code to the alphabet and removing the separators gives
ONCE UPON A TIME
This example is slightly unrealistic since obvious clues were ignored and the quote is quite short. However, all principles of solving a Morbit cipher have been shown so they can be used with any Morbit cipher, regardless of difficulty.
Running Key Cipher
The running key cipher is a variant of the Vigenère Cipher. Rather than using a word as a key, a sentence/paragraph is used as the key. Essentially, instead of repeating a word multiple times as the key, a sentence/paragraph constitutes as the key and is used continuously. If the test was made with Toebes, then the four standard documents used to create a question using the Running Key Cipher are:
- The first line of the Gettysburg Address
- The first line/paragraph of the Declaration of Independence
- The first line of the United States Consitution
- The first line of the Magna Carta (in Latin)
In the event that a question encoded with the running key cipher asks you to decode the phrase but does not give the key for it, then one has to use one of the documents given on the reference sheet (if applicable) and plug them all in to determine which of the documents is the key. If they give the key but do not give the text of the key (ex. "a famous quote by George Washington"), then it is probably best to skip the question.
RSA Cipher
Choose two primes [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math].
Compute [math]\displaystyle{ n = pq }[/math].
Compute the least common multiple of [math]\displaystyle{ p-1 }[/math] and [math]\displaystyle{ q-1 }[/math], and call it [math]\displaystyle{ \lambda(n) }[/math].
Choose an integer [math]\displaystyle{ e }[/math] coprime to [math]\displaystyle{ \lambda(n) }[/math].
Compute the inverse [math]\displaystyle{ d }[/math] of [math]\displaystyle{ e }[/math] modulo [math]\displaystyle{ \lambda(n) }[/math].
Now, say that Alice wants to receive from Bob a message. Alice sends Bob her public key (n, e) through a reliable channel. Bob translates his message M to an integer m, and then converts it to ciphertext using [math]\displaystyle{ c \equiv m^e mod n }[/math].
Alice decodes it using [math]\displaystyle{ m \equiv c^d mod n }[/math].
Sir Arthur Conan Doyle's Cipher from The Adventure of the Dancing Men
While not explicitly stated in the rules, the Dancing Men cipher has appeared in previous tests and possibly may appear as a bonus question in future tests. The Dancing Men cipher is a monoalphabetic substitution cipher with spaces where each letter is represented by a dancing man. A man holding a flag indicates the end of a word. In the story, messages encrypted with this cipher were sent to a woman named Elsie, Sherlock Holmes solved the cipher using that E is the most common letter, and that Elsie's name would likely appear. Since the cipher may be easily decrypted if all the dancing men are memorized, there are a few patterns to help remember them. O and A, R and I, and T and E are flipped. T and E are symmetrical about a vertical axis. N and S have the same legs and right arm. The substitution chart is found below.
An example of the Dancing Men cipher is listed below.
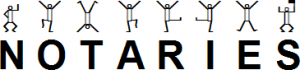 contains the message "NOTARIES", which conveniently shows the patterns listed above.
contains the message "NOTARIES", which conveniently shows the patterns listed above.
Note: The Dancing Men cipher is not included in 2019 rules. However, it is a common part of tests from past years' trial events.
External Links
- Trial event rules
- Cryptogram Workbook (lots of practice problems, 139 pages)
- Mono-alphabetic Substitution Cipher Practice
- Game-like Cryptogram Practice
- Cipher Tools and Practice Tests
North Carolina SO Practice Tests and Keys
Past tests can also be found here. |
| Division B: Hovercraft · Geocaching · Potions and Poisons | Division C: Code Busters · Mystery Design · Remote Sensing |
| Division B: Aerial Scramble · Amazing Mechatronics · Codebusters · Storm the Castle | Division C: Aerial Scramble · Amazing Mechatronics · Environmental Chemistry · Trajectory |